Problems tagged with "linear algebra"
Problem #01
Tags: linear algebra, lecture-02, quiz-02
Let \(\vec x = (1, -2, 5, 0, 3, -1, 4)^T \in\mathbb{R}^7\). What is \(\vec x \cdot\hat{e}^{(3)}\)?
Solution
5.
The "right" way to do this problem is not to calculate the entire dot product, but to recognize that The dot product \(\vec x \cdot\hat{e}^{(3)}\) extracts the third component of \(\vec x\)(which is 5).
Problem #02
Tags: linear algebra, lecture-02, quiz-02
Let \(\hat{u}^{(1)} = \frac{1}{\sqrt{2}}(1, 1)^T\) and \(\hat{u}^{(2)} = \frac{1}{\sqrt{2}}(-1, 1)^T\) form an orthonormal basis \(\mathcal{U}\) for \(\mathbb{R}^2\).
Given \(\vec x = (4, 2)^T\), compute \([\vec x]_{\mathcal{U}}\). That is, compute the coordinates of \(\vec x\) in the new basis.
Solution
\([\vec x]_{\mathcal{U}} = (3\sqrt{2}, -\sqrt{2})^T\).
To find the coordinates of \(\vec x\) in the basis \(\mathcal{U}\), we compute the dot product of \(\vec x\) with each basis vector:
Therefore, the coordinates of \(\vec x\) in the basis \(\mathcal{U}\) are:
Problem #03
Tags: linear algebra, lecture-02, quiz-02
Let \(\hat{u}^{(1)} = \frac{1}{\sqrt{3}}(1, 1, 1)^T\), \(\hat{u}^{(2)} = \frac{1}{\sqrt{2}}(1, -1, 0)^T\), and \(\hat{u}^{(3)} = \frac{1}{\sqrt{6}}(1, 1, -2)^T\) form an orthonormal basis \(\mathcal{U}\) for \(\mathbb{R}^3\).
Given \(\vec x = (3, 1, 2)^T\), compute \([\vec x]_{\mathcal{U}}\). That is, compute the coordinates of \(\vec x\) in the new basis.
Solution
\([\vec x]_{\mathcal{U}} = (2\sqrt{3}, \sqrt{2}, 0)^T\).
To find the coordinates of \(\vec x\) in the basis \(\mathcal{U}\), we compute the dot product of \(\vec x\) with each basis vector:
Therefore, the coordinates of \(\vec x\) in the basis \(\mathcal{U}\) are:
Problem #04
Tags: linear algebra, lecture-02, quiz-02
Let \(\hat{u}^{(1)} = \frac{1}{\sqrt{2}}(1, 0, 1)^T\), \(\hat{u}^{(2)} = (0, 1, 0)^T\), and \(\hat{u}^{(3)} = \frac{1}{\sqrt{2}}(1, 0, -1)^T\) form an orthonormal basis \(\mathcal{U}\) for \(\mathbb{R}^3\).
Given \(\vec x = (2, 3, 4)^T\), compute \([\vec x]_{\mathcal{U}}\). That is, compute the coordinates of \(\vec x\) in the new basis.
Solution
\([\vec x]_{\mathcal{U}} = (3\sqrt{2}, 3, -\sqrt{2})^T\).
To find the coordinates of \(\vec x\) in the basis \(\mathcal{U}\), we compute the dot product of \(\vec x\) with each basis vector:
Therefore, the coordinates of \(\vec x\) in the basis \(\mathcal{U}\) are:
Problem #05
Tags: linear algebra, lecture-02, quiz-02
Let \(\vec x = (2, -3)^T\) and let \(\mathcal{U} = \{\hat{u}^{(1)}, \hat{u}^{(2)}\}\) be an orthonormal basis for \(\mathbb{R}^2\). You are given the following information about the basis vectors:
Compute the coordinates of \(\vec x\) in the basis \(\mathcal{U}\), i.e., compute \([\vec x]_{\mathcal{U}}\).
Solution
\([\vec x]_{\mathcal{U}} = \left(-\frac{6}{5}, -\frac{17}{5}\right)^T\).
The coordinates of \(\vec x\) in basis \(\mathcal{U}\) are given by \([\vec x]_{\mathcal{U}} = (\vec x \cdot\hat{u}^{(1)}, \vec x \cdot\hat{u}^{(2)})^T\). We can compute each dot product using the given information:
Problem #06
Tags: linear algebra, lecture-02, quiz-02
Do the following three vectors form an orthonormal basis for \(\mathbb{R}^3\)? Justify your answer.
Solution
Nope, they don't. The problem is that the second and third vectors are not orthogonal. To be an orthonormal basis, all pairs of vectors must be orthogonal (dot product zero) and each vector must have unit length.
Problem #07
Tags: linear algebra, lecture-02, quiz-02
Do the following three vectors form an orthonormal basis for \(\mathbb{R}^3\)? Justify your answer.
Solution
Nope, they don't. While they are all orthogonal to each other, the second vector does not have unit length (its length is 2). To be an orthonormal basis, all vectors must have unit length.
Problem #08
Tags: linear algebra, lecture-02, quiz-02
Do the following three vectors form an orthonormal basis for \(\mathbb{R}^3\)? Justify your answer.
Solution
Yes.
You can check that all vectors have unit length, and that each pair of vectors is orthogonal (dot product zero).
Problem #15
Tags: linear algebra, lecture-02, quiz-02
Recall that \(\vec x\) is a unit coordinate vector if the sum of the squares of its entries is 1. That is, if \(x_i\) is the \(i\)-th entry of \(\vec x\), then \(\vec x\) is a unit coordinate vector if \(\sum_i x_i^2 = 1\).
True or False: If \(\vec x\) is a unit coordinate vector when expressed in the standard basis, then \([\vec x]_{\mathcal{U}}\) is also a unit coordinate vector when expressed in an orthonormal basis \(\mathcal{U}\).
Solution
True.
The sum of squared entries of a vector is equal to the length of the vector squared. If we express \(\vec x\) in a different basis, we get different coordinates, but it doesn't change the length of the vector itself. So whatever those new coordinates are, their sum of squares must still equal 1.
Problem #16
Tags: linear algebra, lecture-02, quiz-02
True or False: If we express \(\vec x\) in an orthonormal basis \(\mathcal{U}\), the sum of the absolute values of the entries must stay the same. That is, \(\sum_i |x_i| = \sum_i |[\vec x]_{\mathcal{U},i}|\).
Solution
False.
The sum of absolute values (the \(\ell_1\) norm) is not preserved under a change of orthonormal basis. Only the sum of squares (the \(\ell_2\) norm squared) is preserved.
As a counterexample, consider \(\vec x = (1, 0)^T\) in \(\mathbb{R}^2\). The sum of absolute values is \(1\). Now consider the orthonormal basis \(\mathcal{U} = \{\frac{1}{\sqrt{2}}(1, 1)^T, \frac{1}{\sqrt{2}}(-1, 1)^T\}\). Then:
The sum of absolute values is now \(\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} = \sqrt{2}\neq 1\).
Problem #17
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Let \(\vec f(\vec x) = (x_2, -x_1)^T\) be a linear transformation, and let \(\mathcal{U} = \{\hat{u}^{(1)}, \hat{u}^{(2)}\}\) be an orthonormal basis for \(\mathbb{R}^2\) with:
Express the transformation \(\vec f\) in the basis \(\mathcal{U}\). That is, if \([\vec x]_{\mathcal{U}} = (z_1, z_2)^T\), find \([\vec f(\vec x)]_{\mathcal{U}}\) in terms of \(z_1\) and \(z_2\).
Solution
\([\vec f(\vec x)]_{\mathcal{U}} = (z_2, -z_1)^T \).
To express \(\vec f\) in the basis \(\mathcal{U}\), we first need to find what \(\vec f\) does to the basis vectors \(\hat{u}^{(1)}\) and \(\hat{u}^{(2)}\), then express the results in the \(\mathcal{U}\) basis.
To start, we compute \(\vec f(\hat{u}^{(1)})\) and \(\vec f(\hat{u}^{(2)})\).
However, notice that this is \(\vec f(\hat{u}^{(1)})\) and \(\vec f(\hat{u}^{(2)})\) expressed in the standard basis. Therefore, we need to do a change of basis to express these vectors in the \(\mathcal{U}\) basis. We do the change of basis just like we would for any vector: by dotting with each basis vector. That is:
We need to calculate all of these dot products:
Therefore, we have:
Finally, since \(\vec f\) is linear, we can express \(\vec f(\vec x)\) in the \(\mathcal{U}\) basis as:
Problem #18
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Let \(\vec f(\vec x) = (x_1, -x_2, x_3)^T\) be a linear transformation, and let \(\mathcal{U} = \{\hat{u}^{(1)}, \hat{u}^{(2)}, \hat{u}^{(3)}\}\) be an orthonormal basis for \(\mathbb{R}^3\) with:
Express the transformation \(\vec f\) in the basis \(\mathcal{U}\). That is, if \([\vec x]_{\mathcal{U}} = (z_1, z_2, z_3)^T\), find \([\vec f(\vec x)]_{\mathcal{U}}\) in terms of \(z_1\), \(z_2\), and \(z_3\).
Solution
\([\vec f(\vec x)]_{\mathcal{U}} = (-z_2, -z_1, z_3)^T \).
To express \(\vec f\) in the basis \(\mathcal{U}\), we first need to find what \(\vec f\) does to the basis vectors \(\hat{u}^{(1)}\), \(\hat{u}^{(2)}\), and \(\hat{u}^{(3)}\), then express the results in the \(\mathcal{U}\) basis.
To start, we compute \(\vec f(\hat{u}^{(1)})\), \(\vec f(\hat{u}^{(2)})\), and \(\vec f(\hat{u}^{(3)})\).
However, notice that these are expressed in the standard basis. Therefore, we need to do a change of basis to express these vectors in the \(\mathcal{U}\) basis. We do the change of basis just like we would for any vector: by dotting with each basis vector. That is:
We calculate the dot products for \(\vec f(\hat{u}^{(1)})\):
We calculate the dot products for \(\vec f(\hat{u}^{(2)})\):
For \(\vec f(\hat{u}^{(3)})\), we note that \(\vec f(\hat{u}^{(3)}) = (0, 0, 1)^T = \hat{u}^{(3)}\), so:
Therefore, we have:
Finally, since \(\vec f\) is linear, we can express \(\vec f(\vec x)\) in the \(\mathcal{U}\) basis as:
Problem #19
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Let \(\vec f(\vec x) = (x_2, x_1)^T\) be a linear transformation, and let \(\mathcal{U} = \{\hat{u}^{(1)}, \hat{u}^{(2)}\}\) be an orthonormal basis for \(\mathbb{R}^2\) with:
Express the transformation \(\vec f\) in the basis \(\mathcal{U}\). That is, if \([\vec x]_{\mathcal{U}} = (z_1, z_2)^T\), find \([\vec f(\vec x)]_{\mathcal{U}}\) in terms of \(z_1\) and \(z_2\).
Solution
\([\vec f(\vec x)]_{\mathcal{U}} = (z_1, -z_2)^T \).
To express \(\vec f\) in the basis \(\mathcal{U}\), we first compute what \(\vec f\) does to the basis vectors \(\hat{u}^{(1)}\) and \(\hat{u}^{(2)}\).
Now, these results are expressed in the standard basis, and we need to convert them to the \(\mathcal{U}\) basis. In principle, we could do this by dotting with each basis vector, but we can also notice that:
This means we can immediately write:
Finally, since \(\vec f\) is linear:
Problem #20
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Suppose \(\vec f\) is a linear transformation with:
Write the matrix \(A\) that represents \(\vec f\) with respect to the standard basis.
Solution
To make the matrix representing the linear transformation \(\vec f\) with respect to the standard basis, we simply place \(f(\hat{e}^{(1)})\) and \(\vec f(\hat{e}^{(2)})\) as the first and second columns of the matrix, respectively. That is:
Problem #21
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Suppose \(\vec f\) is a linear transformation with:
Write the matrix \(A\) that represents \(\vec f\) with respect to the standard basis.
Solution
To make the matrix representing the linear transformation \(\vec f\) with respect to the standard basis, we simply place \(\vec f(\hat{e}^{(1)})\), \(\vec f(\hat{e}^{(2)})\), and \(\vec f(\hat{e}^{(3)})\) as the columns of the matrix. That is:
Problem #22
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Consider the linear transformation \(\vec f : \mathbb{R}^3 \to\mathbb{R}^3\) that takes in a vector \(\vec x\) and simply outputs that same vector. That is, \(\vec f(\vec x) = \vec x\) for all \(\vec x\).
What is the matrix \(A\) that represents \(\vec f\) with respect to the standard basis?
Solution
You probably could have written down the answer immediately, since this is a very well-known transformation called the identity transformation and the matrix is the identity matrix. But here's why the identity matrix is what it is:
To find the matrix, we need to determine what \(\vec f\) does to each basis vector:
Placing these as columns:
That is the identity matrix we were expecting.
Problem #23
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Suppose \(\vec f\) is represented by the following matrix:
Let \(\vec x = (5, 2)^T\). What is \(\vec f(\vec x)\)?
Solution
\(\vec f(\vec x) = (8, 23)^T\).
Since the matrix \(A\) represents \(\vec f\), we have \(\vec f(\vec x) = A \vec x\). We compute:
Problem #24
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Suppose \(\vec f\) is represented by the following matrix:
Let \(\vec x = (2, 1, -1)^T\). What is \(\vec f(\vec x)\)?
Solution
\(\vec f(\vec x) = (4, -2, 3)^T\).
Since the matrix \(A\) represents \(\vec f\), we have \(\vec f(\vec x) = A \vec x\). We compute:
Problem #25
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Consider the linear transformation \(\vec f : \mathbb{R}^2 \to\mathbb{R}^2\) that rotates vectors by \(90^\circ\) clockwise.
Let \(\mathcal{U} = \{\hat{u}^{(1)}, \hat{u}^{(2)}\}\) be an orthonormal basis with:
What is the matrix \(A\) that represents \(\vec f\) with respect to the basis \(\mathcal{U}\)?
Solution
Remember that the columns of this matrix are:
So we need to compute \(\vec f(\hat{u}^{(1)})\) and \(\vec f(\hat{u}^{(2)})\), then express those results in the \(\mathcal{U}\) basis.
Let's start with \(\vec f(\hat{u}^{(1)})\). \(\vec f\) takes the vector \(\hat{u}^{(1)} = \frac{1}{\sqrt{2}}(1, 1)^T\), which points up and to the right at a \(45^\circ\) angle, and rotates it \(90^\circ\) clockwise, resulting in the vector \(\frac{1}{\sqrt{2}}(1, -1)^T = \hat{u}^{(2)}\)(that is, the unit vector pointing down and to the right at a \(45^\circ\) angle). As it so happens, this is exactly the second basis vector. That is, \(\vec f(\hat{u}^{(1)}) = \hat{u}^{(2)}\).
Now for \(\vec f(\hat{u}^{(2)})\). \(\vec f\) takes the vector \(\hat{u}^{(2)} = \frac{1}{\sqrt{2}}(1, -1)^T\), which points down and to the right at a \(45^\circ\) angle, and rotates it \(90^\circ\) clockwise, resulting in the vector \(\frac{1}{\sqrt{2}}(-1, -1)^T\). This isn't \(\vec f(\hat{u}^{(1)})\), exactly, but it is \(-1\) times \(\hat{u}^{(1)}\). That is, \(\vec f(\hat{u}^{(2)}) = -\hat{u}^{(1)}\).
What we have found is:
Therefore, the matrix is:
Problem #26
Tags: linear algebra, linear transformations, quiz-02, lecture-03
Consider the linear transformation \(\vec f : \mathbb{R}^2 \to\mathbb{R}^2\) that reflects vectors over the \(x\)-axis.
Let \(\mathcal{U} = \{\hat{u}^{(1)}, \hat{u}^{(2)}\}\) be an orthonormal basis with:
What is the matrix \(A\) that represents \(\vec f\) with respect to the basis \(\mathcal{U}\)?
Solution
Remember that the columns of this matrix are:
So we need to compute \(\vec f(\hat{u}^{(1)})\) and \(\vec f(\hat{u}^{(2)})\), then express those results in the \(\mathcal{U}\) basis.
Let's start with \(\vec f(\hat{u}^{(1)})\). \(\vec f\) takes the vector \(\hat{u}^{(1)} = \frac{1}{\sqrt{2}}(1, 1)^T\), which points up and to the right at a \(45^\circ\) angle, and reflects it over the \(x\)-axis, resulting in the vector \(\frac{1}{\sqrt{2}}(1, -1)^T = \hat{u}^{(2)}\)(the unit vector pointing down and to the right at a \(45^\circ\) angle). That is, \(\vec f(\hat{u}^{(1)}) = \hat{u}^{(2)}\).
Now for \(\vec f(\hat{u}^{(2)})\). \(\vec f\) takes the vector \(\hat{u}^{(2)} = \frac{1}{\sqrt{2}}(1, -1)^T\), which points down and to the right at a \(45^\circ\) angle, and reflects it over the \(x\)-axis, resulting in the vector \(\frac{1}{\sqrt{2}}(1, 1)^T = \hat{u}^{(1)}\). That is, \(\vec f(\hat{u}^{(2)}) = \hat{u}^{(1)}\).
What we have found is:
Therefore, the matrix is:
Problem #27
Tags: linear algebra, lecture-02, quiz-02
Let \(\hat{u}^{(1)} = \frac{1}{\sqrt{2}}(1, 1)^T\) and \(\hat{u}^{(2)} = \frac{1}{\sqrt{2}}(1, -1)^T\) form an orthonormal basis \(\mathcal{U}\) for \(\mathbb{R}^2\).
Suppose \([\vec x]_{\mathcal{U}} = (\sqrt{2}, 3\sqrt{2})^T\). That is, the coordinates of \(\vec x\) in the basis \(\mathcal{U}\) are \((\sqrt{2}, 3\sqrt{2})^T\).
What is \(\vec x\) in the standard basis?
Solution
\(\vec x = (4, -2)^T\).
To convert from basis \(\mathcal{U}\) to the standard basis, we compute the linear combination of basis vectors:
Problem #28
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(A = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}\) and let \(\vec v = (1, 1)^T\).
True or False: \(\vec v\) is an eigenvector of \(A\). If true, what is the corresponding eigenvalue?
Solution
True, with eigenvalue \(\lambda = 4\).
We compute:
Since \(A \vec v = 4 \vec v\), the vector \(\vec v\) is an eigenvector with eigenvalue \(4\).
Problem #29
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(A = \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix}\) and let \(\vec v = (1, 2)^T\).
True or False: \(\vec v\) is an eigenvector of \(A\). If true, what is the corresponding eigenvalue?
Solution
False.
We compute:
For \(\vec v\) to be an eigenvector, we would need \(A \vec v = \lambda\vec v\) for some scalar \(\lambda\). This would require:
From the first component, we would need \(\lambda = 4\). From the second component, we would need \(\lambda = \frac{5}{2}\). Since these two values are not equal, there is no such \(\lambda\) that satisfies both equations. Therefore, \(\vec v\) is not an eigenvector of \(A\).
Problem #30
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(A = \begin{pmatrix} 1 & 1 & 3 \\ 1 & 2 & 1 \\ 3 & 1 & 9 \end{pmatrix}\) and let \(\vec v = (1, 4, -1)^T\).
True or False: \(\vec v\) is an eigenvector of \(A\). If true, what is the corresponding eigenvalue?
Solution
True, with eigenvalue \(\lambda = 2\).
We compute:
Since \(A \vec v = 2 \vec v\), the vector \(\vec v\) is an eigenvector with eigenvalue \(2\).
Problem #31
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(A = \begin{pmatrix} 5 & 1 & 1 & 1 \\ 1 & 5 & 1 & 1 \\ 1 & 1 & 5 & 1 \\ 1 & 1 & 1 & 5 \end{pmatrix}\) and let \(\vec v = (1, 2, -2, -1)^T\).
True or False: \(\vec v\) is an eigenvector of \(A\). If true, what is the corresponding eigenvalue?
Solution
True, with eigenvalue \(\lambda = 4\).
We compute:
Since \(A \vec v = 4 \vec v\), the vector \(\vec v\) is an eigenvector with eigenvalue \(4\).
Problem #32
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(A = \begin{pmatrix} 1 & 6 \\ 6 & 6 \end{pmatrix}\) and let \(\vec v = (3, -2)^T\).
True or False: \(\vec v\) is an eigenvector of \(A\). If true, what is the corresponding eigenvalue?
Solution
True, with eigenvalue \(\lambda = -3\).
We compute:
Since \(A \vec v = -3 \vec v\), the vector \(\vec v\) is an eigenvector with eigenvalue \(-3\).
Problem #33
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(\vec v\) be a unit vector in \(\mathbb R^d\), and let \(I\) be the \(d \times d\) identity matrix. Consider the matrix \(P\) defined as:
True or False: \(\vec v\) is an eigenvector of \(P\).
Solution
True.
To verify this, we compute \(P \vec v\):
Since \(P \vec v = -\vec v = (-1) \vec v\), we see that \(\vec v\) is an eigenvector of \(P\) with eigenvalue \(-1\).
Note: The matrix \(P = I - 2 \vec v \vec v^T\) is called a Householder reflection matrix, which reflects vectors across the hyperplane orthogonal to \(\vec v\).
Problem #34
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(A\) be the matrix:
It can be verified that the vector \(\vec{u}^{(1)} = (2, 1)^T\) is an eigenvector of \(A\).
Part 1)
What is the eigenvalue associated with \(\vec{u}^{(1)}\)?
Solution
The eigenvalue is \(\lambda_1 = 6\).
To find the eigenvalue, we compute \(A \vec{u}^{(1)}\):
Therefore, \(\lambda_1 = 6\).
Part 2)
Find another eigenvector \(\vec{u}^{(2)}\) of \(A\). Your eigenvector should have an eigenvalue that is different from \(\vec{u}^{(1)}\)'s eigenvalue. It does not need to be normalized.
Solution
\(\vec{u}^{(2)} = (1, -2)^T\)(or any scalar multiple).
Since \(A\) is symmetric, we know that we can always find two orthogonal eigenvectors. This suggests that we should find a vector orthogonal to \(\vec{u}^{(1)} = (2, 1)^T\) and make sure that it is indeed an eigenvector.
We know from the math review in Week 01 that the vector \((1, -2)^T\) is orthogonal to \((2, 1)^T\)(in general, \((a, b)^T\) is orthogonal to \((-b, a)^T\)).
We can verify:
So the eigenvalue is \(\lambda_2 = 1\), which is indeed different from \(\lambda_1 = 6\).
Problem #35
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(D\) be the diagonal matrix:
Part 1)
What is the top eigenvalue of \(D\)? What eigenvector corresponds to this eigenvalue?
Solution
The top eigenvalue is \(7\).
For a diagonal matrix, the eigenvalues are exactly the diagonal entries. The diagonal entries are \(2, -5, 7\), and the largest is \(7\).
An eigenvector corresponding to this eigenvalue is \(\vec v = (0, 0, 1)^T\).
Part 2)
What is the bottom (smallest) eigenvalue of \(D\)? What eigenvector corresponds to this eigenvalue?
Solution
The bottom eigenvalue is \(-5\).
An eigenvector corresponding to this eigenvalue is \(\vec w = (0, 1, 0)^T\).
Problem #36
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04, linear transformations
Consider the linear transformation \(\vec f : \mathbb{R}^2 \to\mathbb{R}^2\) that reflects vectors over the line \(y = -x\).
Find two orthogonal eigenvectors of this transformation and their corresponding eigenvalues.
Solution
The eigenvectors are \((1, -1)^T\) with \(\lambda = 1\), and \((1, 1)^T\) with \(\lambda = -1\).
Geometrically, vectors along the line \(y = -x\)(i.e., multiples of \((1, -1)^T\)) are unchanged by reflection over that line, so they have eigenvalue \(1\). Vectors perpendicular to the line \(y = -x\)(i.e., multiples of \((1, 1)^T\)) are flipped to point in the opposite direction, so they have eigenvalue \(-1\).
Problem #37
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04, linear transformations
Consider the linear transformation \(\vec f : \mathbb{R}^2 \to\mathbb{R}^2\) that scales vectors along the line \(y = x\) by a factor of 2, and scales vectors along the line \(y = -x\) by a factor of 3.
Find two orthogonal eigenvectors of this transformation and their corresponding eigenvalues.
Solution
The eigenvectors are \((1, 1)^T\) with \(\lambda = 2\), and \((1, -1)^T\) with \(\lambda = 3\).
Geometrically, vectors along the line \(y = x\)(i.e., multiples of \((1, 1)^T\)) are scaled by a factor of 2, so they have eigenvalue \(2\). Vectors along the line \(y = -x\)(i.e., multiples of \((1, -1)^T\)) are scaled by a factor of 3, so they have eigenvalue \(3\).
Problem #38
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04, linear transformations
Consider the linear transformation \(\vec f : \mathbb{R}^2 \to\mathbb{R}^2\) that rotates vectors by \(180°\).
Find two orthogonal eigenvectors of this transformation and their corresponding eigenvalues.
Solution
Any pair of orthogonal vectors works, such as \((1, 0)^T\) and \((0, 1)^T\). Both have eigenvalue \(\lambda = -1\).
Geometrically, rotating any vector by \(180°\) reverses its direction, so \(\vec f(\vec v) = -\vec v\) for all \(\vec v\). This means every nonzero vector is an eigenvector with eigenvalue \(-1\).
Since we need two orthogonal eigenvectors, any orthogonal pair will do.
Problem #39
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Consider the diagonal matrix:
How many unit length eigenvectors does \(A\) have?
Solution
\(\infty\) The upper-left \(2 \times 2\) block of \(A\) is the identity matrix. Recall from lecture that the identity matrix has infinitely many eigenvectors: every nonzero vector is an eigenvector of the identity with eigenvalue 1.
Similarly, any vector of the form \((a, b, 0)^T\) where \(a\) and \(b\) are not both zero satisfies:
So any such vector is an eigenvector with eigenvalue 1. There are infinitely many unit vectors of this form (they form a circle in the \(x\)-\(y\) plane), so \(A\) has infinitely many unit length eigenvectors.
Additionally, \((0, 0, 1)^T\) is an eigenvector with eigenvalue 5.
Problem #40
Tags: linear algebra, quiz-03, spectral theorem, eigenvectors, lecture-04
Consider the matrix:
True or False: The spectral theorem guarantees that \(A\) has 2 orthogonal eigenvectors.
Solution
False.
The spectral theorem only applies to symmetric matrices. The matrix \(A\) is not symmetric because \(A^T \neq A\):
Since \(A\) is not symmetric, the spectral theorem does not apply, and we cannot use it to conclude anything about \(A\)'s eigenvectors.
Problem #41
Tags: linear algebra, quiz-03, spectral theorem, eigenvectors, lecture-04
Suppose \(A\) is a symmetric matrix, and \(\vec{u}^{(1)}\) and \(\vec{u}^{(2)}\) are both eigenvectors of \(A\).
True or False: \(\vec{u}^{(1)}\) and \(\vec{u}^{(2)}\) must be orthogonal.
Solution
False.
Consider the identity matrix \(I\). Every nonzero vector is an eigenvector of \(I\) with eigenvalue 1. For example, both \((1, 0)^T\) and \((1, 1)^T\) are eigenvectors of \(I\), but they are not orthogonal:
The spectral theorem says that you can find\(n\) orthogonal eigenvectors for an \(n \times n\) symmetric matrix, but it does not say that every pair of eigenvectors is orthogonal.
Aside: It can be shown that if \(\vec{u}^{(1)}\) and \(\vec{u}^{(2)}\) have different eigenvalues, then they must be orthogonal.
Problem #42
Tags: linear algebra, quiz-03, spectral theorem, eigenvectors, diagonalization, lecture-04
Suppose \(A\) is a \(d \times d\) symmetric matrix.
True or False: There exists an orthonormal basis in which \(A\) is diagonal.
Solution
True.
By the spectral theorem, every \(d \times d\) symmetric matrix has \(d\) mutually orthogonal eigenvectors. If we normalize these eigenvectors, they form an orthonormal basis.
In this eigenbasis, the matrix \(A\) is diagonal: the diagonal entries are the eigenvalues of \(A\).
Problem #43
Tags: linear algebra, quiz-03, symmetric matrices, eigenvectors, lecture-04, linear transformations
The figure below shows a linear transformation \(\vec{f}\) applied to points on the unit circle. Each arrow shows the direction and relative magnitude of \(\vec{f}(\vec{x})\) for a point \(\vec{x}\) on the circle.
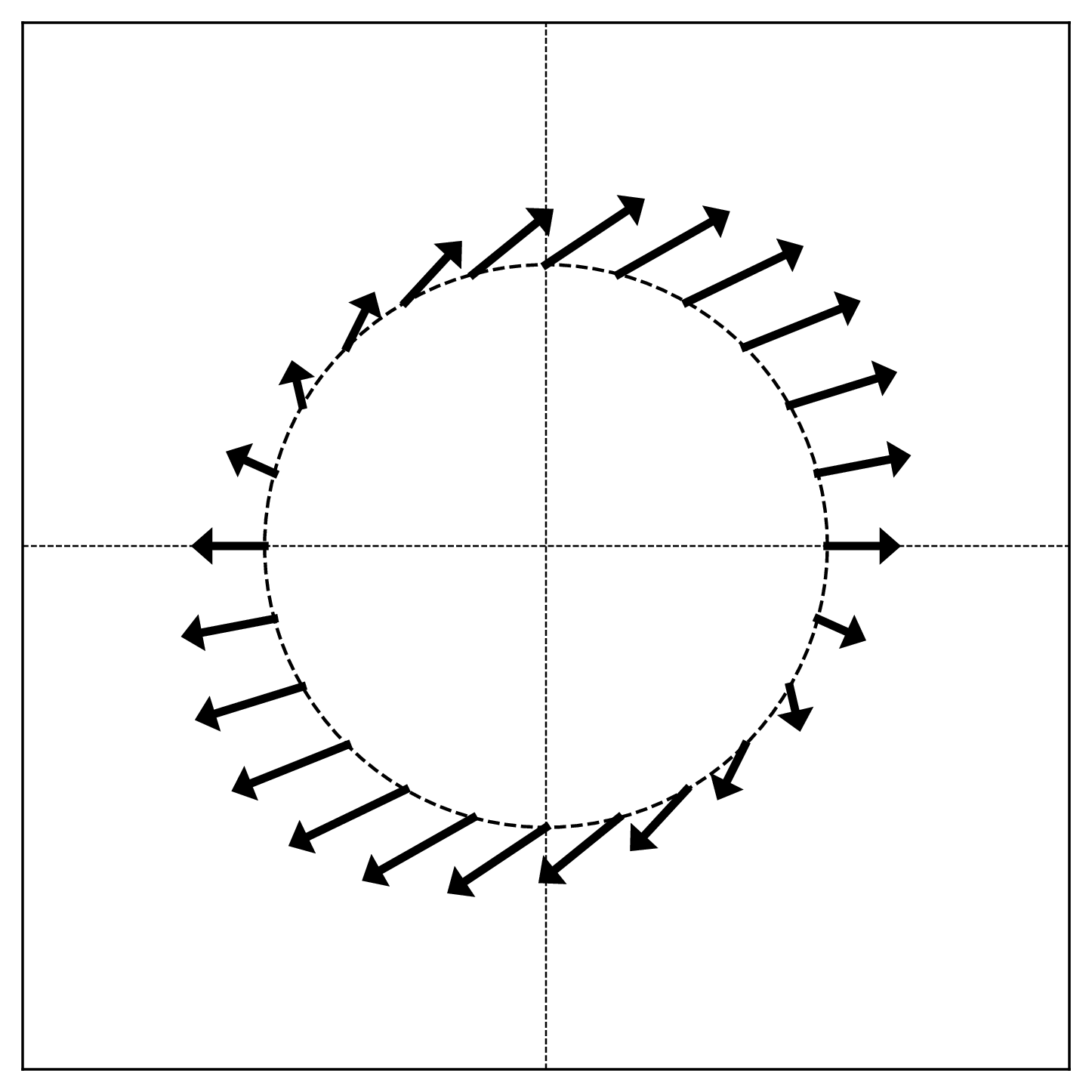
True or False: The linear transformation \(\vec{f}\) is symmetric.
Solution
False.
Recall from lecture that symmetric linear transformations have orthogonal axes of symmetry. In the visualization, this would appear as two perpendicular directions where the arrows point directly outward (or inward) from the circle.
In this figure, there are no such orthogonal axes of symmetry. The pattern of arrows does not exhibit the characteristic symmetry of a symmetric transformation.
Problem #44
Tags: linear algebra, quiz-03, diagonal matrices, eigenvectors, lecture-04, linear transformations
The figure below shows a linear transformation \(\vec{f}\) applied to points on the unit circle. Each arrow shows the direction and relative magnitude of \(\vec{f}(\vec{x})\) for a point \(\vec{x}\) on the circle.
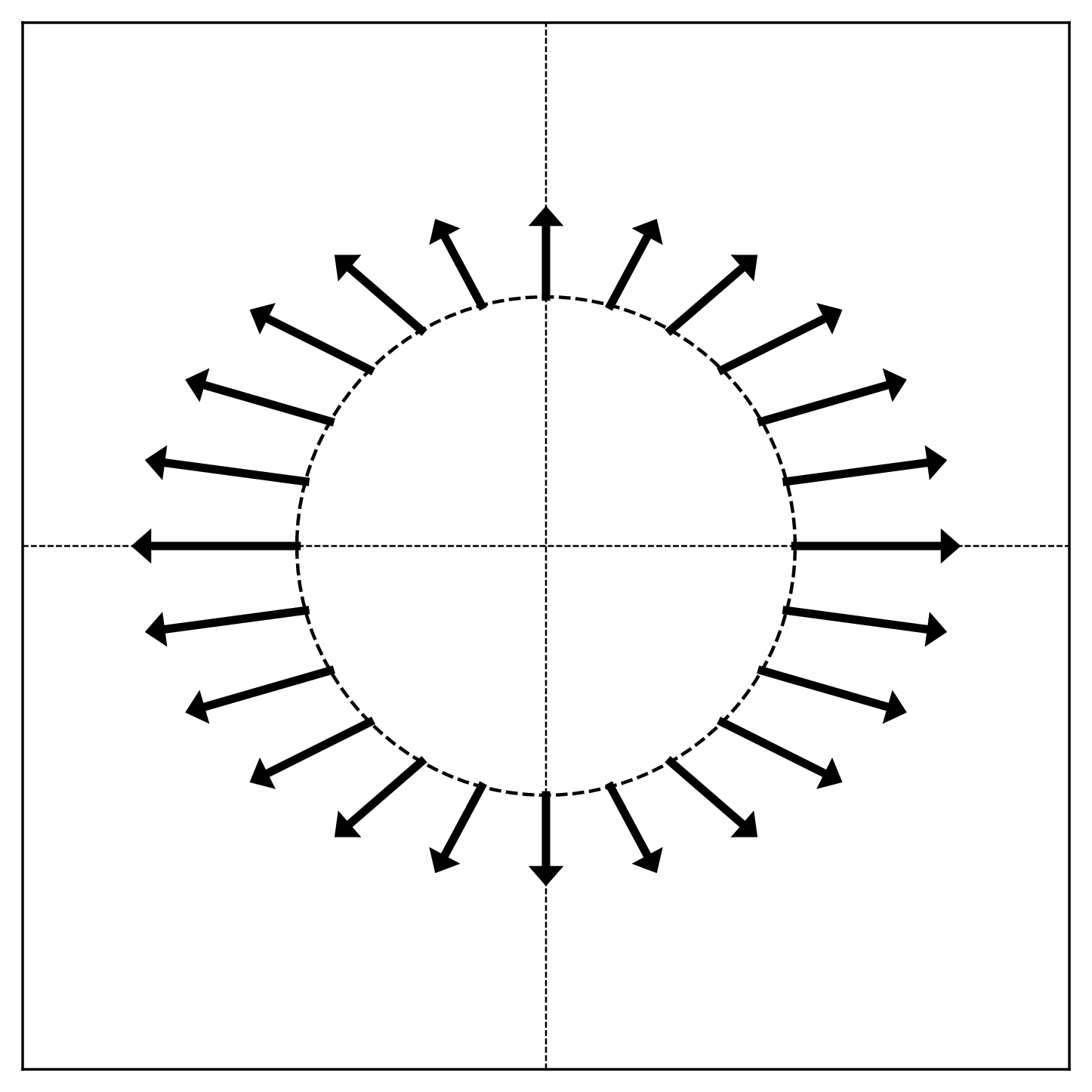
True or False: The matrix representing \(\vec{f}\) with respect to the standard basis is diagonal.
Solution
True.
A matrix is diagonal if and only if the standard basis vectors are eigenvectors. In the visualization, eigenvectors correspond to directions where the arrows point radially (directly outward or inward).
Looking at the figure, the arrows at \((1, 0)\) and \((-1, 0)\) point horizontally, and the arrows at \((0, 1)\) and \((0, -1)\) point vertically. This means the standard basis vectors \(\hat e^{(1)} = (1, 0)^T\) and \(\hat e^{(2)} = (0, 1)^T\) are eigenvectors.
Since the standard basis vectors are eigenvectors, the matrix is diagonal in the standard basis.
Problem #45
Tags: linear algebra, eigenbasis, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(\vec{u}^{(1)}, \vec{u}^{(2)}, \vec{u}^{(3)}\) be three unit length orthonormal eigenvectors of a linear transformation \(\vec{f}\), with eigenvalues \(8\), \(4\), and \(-3\) respectively.
Suppose a vector \(\vec{x}\) can be written as:
What is \(\vec{f}(\vec{x})\), expressed in coordinates with respect to the eigenbasis \(\{\vec{u}^{(1)}, \vec{u}^{(2)}, \vec{u}^{(3)}\}\)?
Solution
\([\vec{f}(\vec{x})]_{\mathcal{U}} = (16, -12, -3)^T\) Using linearity and the eigenvector property:
Since \(\vec{u}^{(1)}\) is an eigenvector with eigenvalue \(8\), we have \(\vec{f}(\vec{u}^{(1)}) = 8\vec{u}^{(1)}\). Similarly, \(\vec{f}(\vec{u}^{(2)}) = 4\vec{u}^{(2)}\) and \(\vec{f}(\vec{u}^{(3)}) = -3\vec{u}^{(3)}\):
In the eigenbasis, this is simply \((16, -12, -3)^T\).
Problem #46
Tags: linear algebra, eigenbasis, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(\vec{u}^{(1)}, \vec{u}^{(2)}, \vec{u}^{(3)}\) be three unit length orthonormal eigenvectors of a linear transformation \(\vec{f}\), with eigenvalues \(5\), \(-2\), and \(3\) respectively.
Suppose a vector \(\vec{x}\) can be written as:
What is \(\vec{f}(\vec{x})\), expressed in coordinates with respect to the eigenbasis \(\{\vec{u}^{(1)}, \vec{u}^{(2)}, \vec{u}^{(3)}\}\)?
Solution
\([\vec{f}(\vec{x})]_{\mathcal{U}} = (20, -2, -6)^T\) Using linearity and the eigenvector property:
Since \(\vec{u}^{(1)}\) is an eigenvector with eigenvalue \(5\), we have \(\vec{f}(\vec{u}^{(1)}) = 5\vec{u}^{(1)}\). Similarly, \(\vec{f}(\vec{u}^{(2)}) = -2\vec{u}^{(2)}\) and \(\vec{f}(\vec{u}^{(3)}) = 3\vec{u}^{(3)}\):
In the eigenbasis, this is simply \((20, -2, -6)^T\).
Problem #47
Tags: optimization, linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(A\) be a symmetric matrix with eigenvalues \(6\) and \(-9\).
True or False: The maximum value of \(\|A\vec{x}\|\) over all unit vectors \(\vec{x}\) is \(6\).
Solution
False. The maximum is \(9\).
The maximum of \(\|A\vec{x}\|\) over unit vectors is achieved when \(\vec{x}\) is an eigenvector corresponding to the eigenvalue with the largest absolute value.
Here, \(|-9| = 9 > 6 = |6|\), so the maximum is achieved at the eigenvector with eigenvalue \(-9\).
If \(\vec{u}\) is a unit eigenvector with eigenvalue \(-9\), then:
Problem #48
Tags: optimization, linear algebra, quiz-03, eigenvalues, eigenvectors, quadratic forms, lecture-04
Let \(A\) be a \(3 \times 3\) symmetric matrix with the following eigenvectors and corresponding eigenvalues: \(\vec{u}^{(1)} = \frac{1}{3}(1, 2, 2)^T\) has eigenvalue \(4\), \(\vec{u}^{(2)} = \frac{1}{3}(2, 1, -2)^T\) has eigenvalue \(1\), and \(\vec{u}^{(3)} = \frac{1}{3}(2, -2, 1)^T\) has eigenvalue \(-10\).
Consider the quadratic form \(\vec{x}\cdot A\vec{x}\).
Part 1)
What unit vector \(\vec{x}\) maximizes \(\vec{x}\cdot A\vec{x}\)?
Solution
\(\vec{u}^{(1)} = \frac{1}{3}(1, 2, 2)^T\) The quadratic form \(\vec{x}\cdot A\vec{x}\) is maximized by the eigenvector with the largest eigenvalue. Among \(4\), \(1\), and \(-10\), the largest is \(4\), so the maximizer is \(\vec{u}^{(1)}\).
Part 2)
What is the maximum value of \(\vec{x}\cdot A\vec{x}\) over all unit vectors?
Solution
\(4\) The maximum value equals the largest eigenvalue. We can verify:
Part 3)
What unit vector \(\vec{x}\) minimizes \(\vec{x}\cdot A\vec{x}\)?
Solution
\(\vec{u}^{(3)} = \frac{1}{3}(2, -2, 1)^T\) The quadratic form is minimized by the eigenvector with the smallest eigenvalue. Among \(4\), \(1\), and \(-10\), the smallest is \(-10\), so the minimizer is \(\vec{u}^{(3)}\).
Part 4)
What is the minimum value of \(\vec{x}\cdot A\vec{x}\) over all unit vectors?
Solution
\(-10\) The minimum value equals the smallest eigenvalue. We can verify:
Problem #49
Tags: linear algebra, quiz-03, eigenvalues, eigenvectors, lecture-04
Let \(A\) be a symmetric matrix with top eigenvalue \(\lambda\). Let \(B = A + 5I\), where \(I\) is the identity matrix.
True or False: The top eigenvalue of \(B\) must be \(\lambda + 5\).
Solution
True.
The main thing to realize is that \(A\) and \(B\) have the same eigenvectors. If \(\vec v\) is an eigenvector of \(A\) with eigenvalue \(\lambda\), then:
Thus, \(\vec v\) is also an eigenvector of \(B\) with eigenvalue \(\lambda + 5\).
This means that the eigenvalues of \(B\) are simply the eigenvalues of \(A\) shifted by 5. Therefore, if \(\lambda\) is the top eigenvalue of \(A\), then \(\lambda + 5\) is the top eigenvalue of \(B\).